[ML] 뉴턴-랩슨법(Newton's Method)을 쓰는 이유

---

0. 들어가는 글

데이터 분석을 하다보면 종종 뉴턴 방법(Newton's method) 또는 뉴턴-랩슨법(Newton-raphson's method)을 만나는 경우가 있습니다.

뉴턴-랩슨법은 해(Solution)을 구하는 방법으로 알려져 있긴 합니다.해를 구할 때 뉴턴-랩슨법을 직접 사용하는 경우도 있고, 개념을 차용하기도 합니다.

대표적으로 딥러닝에서 경사하강법(Gradient descent)을 들 수 있겠네요.

아무튼 다양한 분야에서 활용되고 있는 뉴턴-랩슨법을 소개하려고 합니다.

알아두면 생각보다 유용하거든요.

 

 

---

 

 

1. 해(Solution)을 구하는 방법?

앞서 말한대로 뉴턴-랩슨법은 해(Solution)를 구하는 방법 중 하나입니다.

구체적으로는 함수값을 0으로 만들어주는 값을 찾을 때 꽤 유용하고 널리 활용됩니다.

 

우리, 중학교 수학에서 배운 걸 잠시 떠올려봅시다. 아래와 같은 이차방정식이 하나 있다고 해볼게요.

$$ \begin{align} x^{2} + x - 12 = 0 \end{align}$$

이차방정식을 풀기 위해서는 보통 인수분해나 근의 공식을 활용하는 걸 배웁니다.

인수분해로 활용해서 한 번 풀어보겠습니다. 

$$
\begin{align} x^{2} + x - 12 = 0 \\[15pt]
\Leftrightarrow (x+4)(x-3) = 0 \\[15pt]
\therefore x = -4 \; or \;3 \end{align}
$$

 

이차방정식을 배우고 난 뒤에는 이차함수를 배웁니다.

우리가 배운 이차방정식을 이차함수로 확장해볼 수도 있어요.

아래와 같은 이차함수가 있다고 해보겠습니다.

$$ \begin{align} f(x) = y = x^{2} + x - 12 \end{align}$$

 

이 함수를 그려보면 그림처럼 포물선을 그릴 겁니다.

식 $x^{2} + x - 12$는 $x$에 따라 가질 수 있는 값이 굉장히 다양합니다.

$x$에 $2$를 넣으면 $-6$이 나오고, $x$에 $4$를 넣으면 $8$이 될 겁니다.

그렇다면 식을 0으로 만들어주는 $x$를 찾아볼 수도 있을 겁니다.

그래프를 보고 직접 찾아보면 아래처럼 $x = -4$일 때, 그리고 $x = 3$일 때 식 $x^{2} + x - 12$은 $0$이 됩니다.

 

즉 이차방정식 $ x^{2} + x - 12 = 0$을 푸는 문제는 이차함수 $y = x^{2} + x -12 $에서 $ y = 0 $를 만족하는 함수값을 찾는 문제는 동일한 문제입니다. 이처럼 우리가 풀고자 하는 문제(해를 구하는 문제)는 함수에 대응하여 풀어볼 수 있습니다.

하지만 이차방정식은 아주 풀기 쉬운 문제에 속합니다.

무엇보다 근의 공식이라는 막강한 풀이가 있으니까요.

대부분 문제는 풀기 어려울 뿐더러, 풀이방법 자체가 알려지지 않은 경우가 많습니다. 

 

그렇다고 포기할 수는 없으니, 이럴 때는 정공법으로 갑니다.

대입할 수 있는 모든 값을 다 넣어보면 결국엔 답을 얻을 수 있을 거에요(!).

다만, '모든 값'이라는 건 정말 무한한 계산을 해야 한다는 의미입니다. 

기왕이면 효율적으로 수행하는 게 좋겠지요.

불필요한 경우를 제외한 숫자를 대입해서 효율적으로 해를 찾아주는 방법이 바로 뉴턴-랩슨법입니다.

 

 

---

 

 

2. 뉴턴랩슨법의 기본 개념

아래 그림과 같은 함수가 있습니다.

우리의 목표는 이 함수를 0으로 만들어주는 값, 해(Solution)를 찾는 겁니다.

앞서 말한대로 정공법으로 가겠습니다.

값을 계속 대입해서 함수값을 0으로 만들어주는 경우를 찾아볼 겁니다.

 

예를 들어서 1, 2, 3, $\cdots$, 100 등을 차례차례 넣어본다고 해볼게요.

직접 손으로 계산해보다보면, 이런 고민이 들 거에요.

이 방향대로(=값을 계속 키워서) 계산하다보면 0이 나오기는 할까?

 

위의 함수는 증가함수처럼 보여요.  값을 계속 키우면 영영 0에 도달하지 못할 거에요.

 

반대로 100부터 줄여나간다고 해보겠습니다.

100, 99, 98, 97, $\cdots$, 1 이런 식으로 값을 넣어 볼게요.

이번에는 이런 고민이 들 겁니다.

만약 해가 2.35 같이 소수점이 있는 경우면 어떡하지?

 

이런 경우에 대비해서 0.01 단위로 숫자를 넣어볼 수 있습니다.
그렇다면 100, 99.99, 99.98, 99.97, $\cdots$, 0.03, 0.02, 0.01 이런 식으로 넣어볼 수 있겠네요.

하지만 해가 2.35가 아니라 2.353, 2.3531 처럼 아주 작은 숫자가 아니라는 보장도 없지요.

모든 경우에 대비하려고 아주 작은 단위로 숫자를 넣으면 계산 횟수가 너무 많아집니다.

 

즉 효율적으로 값을 넣어서 해를 구하기 위해서는

① 다음에 넣을 값의 방향을 정해야 하고(더 큰 값을 넣을지, 작은 값을 넣을지)

② 다음에 넣을 값의 크기도 조절해야 합니다.

 

 

---

 

우선 첫번째 고민부터 해결해보겠습니다.

아래처럼 3개의 값이 있다고 해보겠습니다. 

 

 

맨 처음 넣는 값을 $b$라고 해볼게요.

그리고 $a$를 넣어보고 계산하고, $c$를 넣어보고 계산해볼 수 있습니다.

계산할 결과 중에, 값이 작아지는 방향을 택하면 될 거에요. 우리의 목표는 함수값이 0으로 도달하는 거니까요.

이렇게 양 옆의 값을 대조하는 방식보다, 조금 더 세련된 방법이 있습니다.

바로 접선의 기울기를 구하면 됩니다. 

 

$x = b$ 일때의 접선의 기울기를 그려보겠습니다. 

눈으로 볼 수 있듯이 기울기가 양수입니다.

기울기가 양수라는 말은 값을 키울 수록 함수값은 더 커진다는 의미겠지요.

즉 접선의 기울기 부호와 '반대로' 움직이면 됩니다.

 

 

---

 

이제 두번째 고민을 해결해보겠습니다.

다음에 넣는 값의 크기를 적절히 조절해볼 거에요. 

해에 가까워질수록 촘촘하게, 작은 단위의 숫자를 넣을 수 있도록 하는 겁니다.

접선의 기울기를 그대로 이용 할건데요, 접선을 $x$축 방향으로 쭉 그려보겠습니다.

 

이 때 $x$축과 맞닿은 점을 $a^{*}$라고 하겠습니다.

$b$ 다음에 $a$를 넣는 것보다는 $a^{*}$를 넣는 게 훨씬 해에 가까운 값을 넣는 것처럼 보입니다.

 

이제 새로운 $a^{*}$를 $b$라고 생각해볼게요.

그렇다면 새로운 접선의 기울기(아래 그림의 빨간색 실선)를 구할 수 있고, 새로운 접선이 $x$축과 맞닿은 점 $a^{**}$도 구할 수 있을 겁니다.

그림으로 그려보겠습니다.

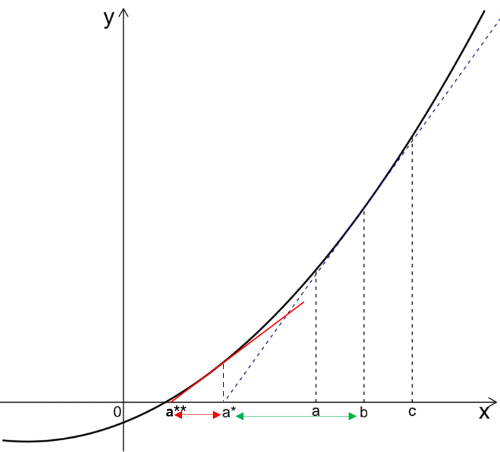
확실히 해(Solution)에 근접한 것을 볼 수 있습니다. 

특히 처음 계산했을 때의 간격(초록색 양방향 화살표)에 비해

두번째로 계산했을 때의 간격(빨간색 양방향 화살표)은 더 작아졌어요. 

아마도 계산을 반복하면 이 간격이 더 좁아질 거라고 예상됩니다.

 

이런 방식으로 다음 값을 계산해서 해를 구하는 과정을 뉴턴-랩슨법이라고 합니다.

값을 넣어서 해를 구할 때 생기는 두 가지 고민이 모두 해결됐네요.

접선의 기울기를 활용해서 다음 값의 방향과 크기를 정하면 되니까요.

 

 

---

 

3. 이제, 일반화를 해볼게요.

처음에 넣는 값을 $x_t$, 함수 $f(x)$에 $x_t$를 넣은 값을 $f(x_t)$라고 하겠습니다.

그리고 $x_t$에서 접선의 기울기를 $f'(x_{t})$라고 할게요. 보통은 미분을 해서 구하니까요.

그리고 다음에 넣을 값을 $x_{t+1}$이라고 해하겠습니다.

위 챕터에서 본 함수의 상황에 대입해보면 아래 그림과 같습니다. 

 

 

 

이 그림을 수식으로 표현해보겠습니다.

우선 $x_t$에서 접선의 기울기 $f'(x_t)$는 다음과 같이 나타낼 수 있어요.

$$ \frac{f(x_t) - 0}{x_{t} - x_{t+1}} = f'(x_t) $$ 

 

식을 $x_{t+1}$로 정리하면 다음과 같이 구할 수 있습니다.

$$ x_{t+1} = x_t - \frac{f(x_t)}{f'(x_t)} $$

 

이제 다음에 넣을 값 $x_{t+1}$을 어떻게 구할 지 정할 수 있게 되었네요. 

이 과정을 함수값이 0에 가까울 때 까지 계산을 반복해주면 됩니다.

종종 함수값이 아니라 $x_{t}$와 $x_{t+1}$의 간격이 임의의 양수($\epsilon$)보다 작은 경우까지 반복해주기도 합니다.

 

이를 실제로 구현한 코드는 부록을 참고하시기 바랍니다.

---